Machine Learning Course Summary (Part 3)

 

Summary from the Stanford's Machine learning class by Andrew Ng

---

• Part 1
  • Supervised vs. Unsupervised learning, Linear Regression, Logistic Regression, Gradient Descent
• Part 2
  • Regularization, Neural Networks
• Part 3
  • Debugging and Diagnostic, Machine Learning System Design
• Part 4
  • Support Vector Machine, Kernels
• Part 5
  • K-means algorithm, Principal Component Analysis (PCA) algorithm
• Part 6
  • Anomaly detection, Multivariate Gaussian distribution
• Part 7
  • Recommender Systems, Collaborative filtering algorithm, Mean normalization
• Part 8
  • Stochastic gradient descent, Mini batch gradient descent, Map-reduce and data parallelism

---

Debugging & Diagnostics

• Evaluating a Hypothesis
  • What if the hypothesis fails to generalize to new examples not in training set?
  • Divide the dataset into Train set, Cross Validation st and Test set

• Bias vs. Variance
  • Underfit, Just Right and Overfit graphs.

• Error graph comparing Cross validation error and Training error

• How to identify if it is a bias problem or a variance problem?

• Regularization and bias/variance
  • Large, Intermediate and Small lamda values.

• Choosing the regularization parameter “lamda”:

• Learning Curves

• Debugging 
  • Suppose you have implemented regularized linear regression to predict housing prices.
    However, when you test your hypothesis on a new set of houses, you find that it makes unacceptably large errors in its predictions. What should you try next?
    • Get more training examples ?  Fixes High Variance 
    • Try smaller sets of features ?  Fixes High Variance 
    • Try getting additional features ?  Fixes High Bias
    • Try adding polynomial features ?  Fixes High Bias
    • Try decreasing lamda ?  Fixes High Bias
    • Try increasing lamda ? Fixes High Variance 

• Neural networks and overfitting

Machine Learning System Design

• Prioritize What to work on
  • Spend your time to make it have low error
    • Collect lots of data (e.g. “honeypot” project)
    • Develop sophisticated features
    • Develop sophisticated algorithms
  • Error Analysis
    • Start with simple algorithm that you can implement quickly.
    • Plot learning curves to decide if more data, more feature etc. is likely to help.
    • Manually examine the examples in Cross Validation set, which our algorithm made errors on. See if we can find any systematic trend.
• Error Metrics for Skewed classes
  • Use this when you have more number of positive examples than negative examples.
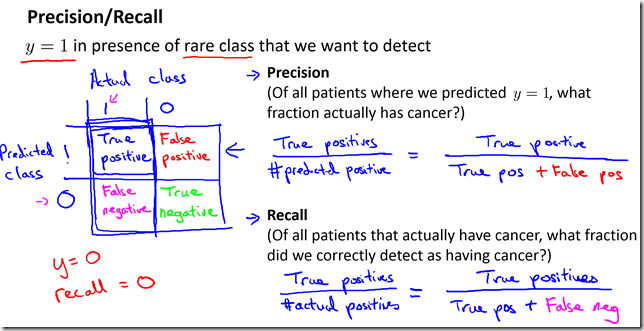
  • Precision / Recall
    • A classifier with high precision and high recall is good, even if we have very skewed classes.

• F₁ Score (F Score)

• Large Data Rationale
  • “It’s not who has the best algorithm that wins. It’s who has the most data.”