Machine Learning Course Summary (Part 2)

 

Summary from the Stanford's Machine learning class by Andrew Ng

---

• Part 1
  • Supervised vs. Unsupervised learning, Linear Regression, Logistic Regression, Gradient Descent
• Part 2
  • Regularization, Neural Networks
• Part 3
  • Debugging and Diagnostic, Machine Learning System Design
• Part 4
  • Support Vector Machine, Kernels
• Part 5
  • K-means algorithm, Principal Component Analysis (PCA) algorithm
• Part 6
  • Anomaly detection, Multivariate Gaussian distribution
• Part 7
  • Recommender Systems, Collaborative filtering algorithm, Mean normalization
• Part 8
  • Stochastic gradient descent, Mini batch gradient descent, Map-reduce and data parallelism

---

Regularization

• Problem of Overfitting

• Options to address overfitting:
  • Reduce number of features
    • Manually select which features to keep
    • Model selection algorithm (later in course)
  • Regularization
    • Keep all features but reduce magnitude/values of parameters theta.
    • works well when we have lots of features, each of which contributes a bit to predicting y.
• Too much regularization can “underfit” the training set and this can lead to worse performance even for examples not in the training set.

• Cost Function
  • if lamda is too large (e.g. 10¹⁰) than the algorithm results in “underfitting”(fails to fit even training set)

• Regularization with Liner Regression

• Normal Equation

• Regularization with Logistic Regression

Neural Networks

• Introduction

  • Algorithms that try to mimic the brain. Was very widely used in 80s and early 90s; popularity diminished in late 90s.

  • Send a signal to any brain sensor and it will learn to deal with it. E.g. Auditory cortex learns to see, Somatosensory cortex learn to see.
    Seeing with your tongue, human echolocation, third eye for frog.
    

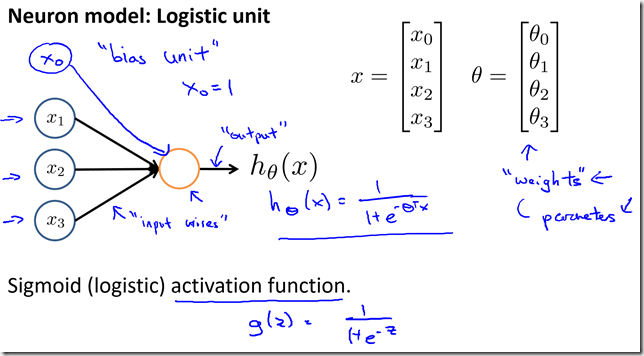
• Model Representation

• Forward propagation

• Non-linear classification example: XOR/XNOR

• Non-linear classification example: AND

• Non-linear classification example: OR

• XNOR

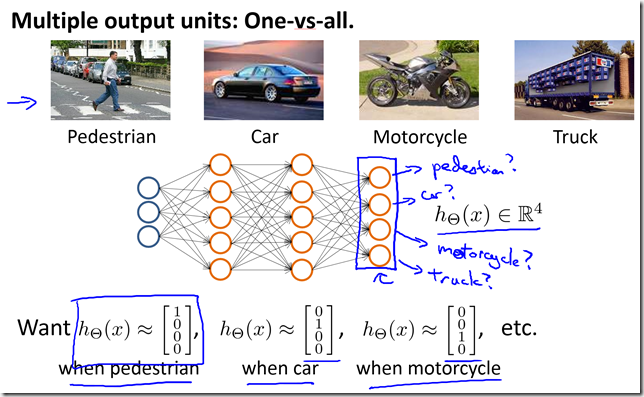
• Multi-class classification

• Cost Function

• Unlike logistic regression we DO NOT sum the value of “Bias Unit” in the regularization term for cost of neural networks.
• Just as logistic regression a large value of “lamda” will penalize large parameter values, thereby, reducing the changes of overfitting the training set.

• Backpropagation algorithm

• Unrolling parameters

• Gradient Checking
  • There may be bugs in forward/back propagation algorithms even if the cost function looks correct.
  • Gradient checking helps identify these bugs.

• Implementation Note:
  • Implement backprop to compute DVec (unrolled ).
  • Implement numerical gradient check to compute gradApprox.
  • Make sure they give similar values.
  • Turn off gradient checking. Using backprop code for learning
• Be sure to disable your gradient checking code before training your classifier. If you run numerical gradient computation on
  every iteration of gradient descent (or in the inner loop of costFunction(…))your code will be very slow.

• Random initialization
  • Initializing theta to 0 works for logistic regression but it does not work for neural network.
  • If we initialize theta to 0 than for neural network, after each update, parameters corresponding to inputs going to each of two hidden units are identical.
  • This causes the “Problem of Symmetric Weight”
  • To solve this issue randomly initialize the theta values.

• Training a neural network