Machine Learning Course Summary (Part 4)

Summary from the Stanford's Machine learning class by Andrew Ng

---

• Part 1
  • Supervised vs. Unsupervised learning, Linear Regression, Logistic Regression, Gradient Descent
• Part 2
  • Regularization, Neural Networks
• Part 3
  • Debugging and Diagnostic, Machine Learning System Design
• Part 4
  • Support Vector Machine, Kernels
• Part 5
  • K-means algorithm, Principal Component Analysis (PCA) algorithm
• Part 6
  • Anomaly detection, Multivariate Gaussian distribution
• Part 7
  • Recommender Systems, Collaborative filtering algorithm, Mean normalization
• Part 8
  • Stochastic gradient descent, Mini batch gradient descent, Map-reduce and data parallelism

---

Support Vector Machines

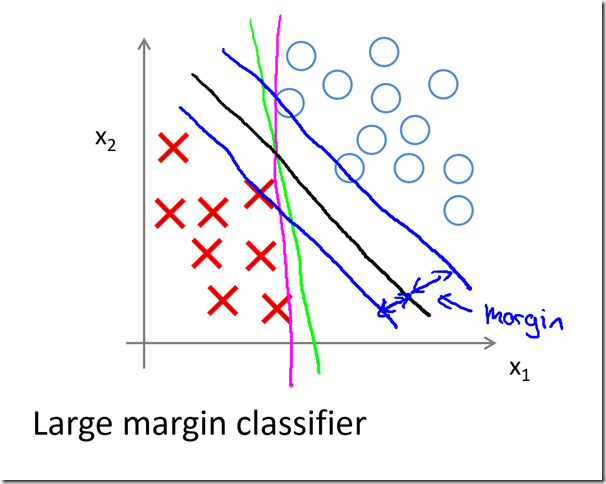
• Hypothesis and Decision Boundary 
  • Hypothesis 

• Decision Boundary

• Kernels
  • For Non Linear Decision Boundary we can use higher order polynomials but is there a different/better choice of the features ?
  • High order polynomials can be computationally heavy for image processing type problem.
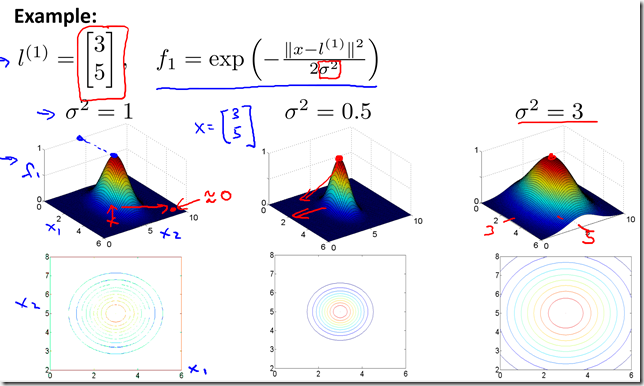
  • Given X, compute new feature depending  on proximity to landmarks.

• When x = 3/5 the bump increases as its near to the landmark l(1), which is equal to [3,5], sigma square value makes the bump narrow or wide.

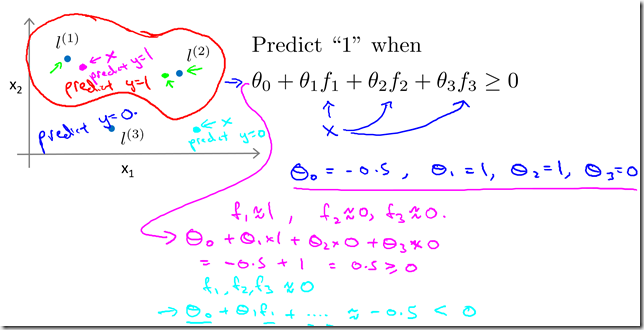
• Predict “1” when theta0 + theta1 f1 + theta2 f2 + theta3 f3  >= 0
• Let’s assume theta0 = -0.5, theta1 = 1, theta2 = 1, theta3 = 0
• For x(1),
  • f1 == 1 ( as its close to l(1))
  • f2 == 0 ( as its close to l(2))
  • f3 == 0 ( as its close to l(3))
• Hypothesis :
  • = theta0 + theta1 * 1 + theta2 * 0 + theta3 * 0
  • = -0.5 + 1
  • = 0.5  (which is > 0, so we predict 1 )

• How do we choose Landmarks ??
• What other similarity functions we can use other than ‘Gaussian Kernel” ??
  • * Make l same as X

• Kernels do not go well with logistic regression due to computational complexity
• SVM with Kernels are optimized for computation and runs much faster

Using SVM

Use software packages (liblinear, libsvm, …) to solve for parameters theta.

Need to Specify:

• Choice of parameter C
• Choice of Kernel (similarity function)
  1. No Kernel (“linear kernel”)
     • Predict “y=1” if theta transpose x > 0
     • No landmarks or features f(i) from x.
     • Choose this when n is large and m is small. (Number of features is large and training examples are less)
  2. Gaussian Kernel
     • Predict “y=1” if theta transpose f > 0
     • Use landmarks
     • Need to choose sigma square
     • Choose this when n is small and m is large. ( very large training set but small number of features)
     • Do perform feature scaling before using the Gaussian kernel
  3. Other choices
     • All similarity function need to satisfy a technical condition called “Mercers Theorem”
     • Polynomial kernel
     • More esoteric:
       1. string kernel
       2. chi-square kernel
       3. historgram intersection kernel

Many SVM packages already have built-in multi class classification functionality, if not use the one-vs-all method

• Logistic Regression vs. SVM